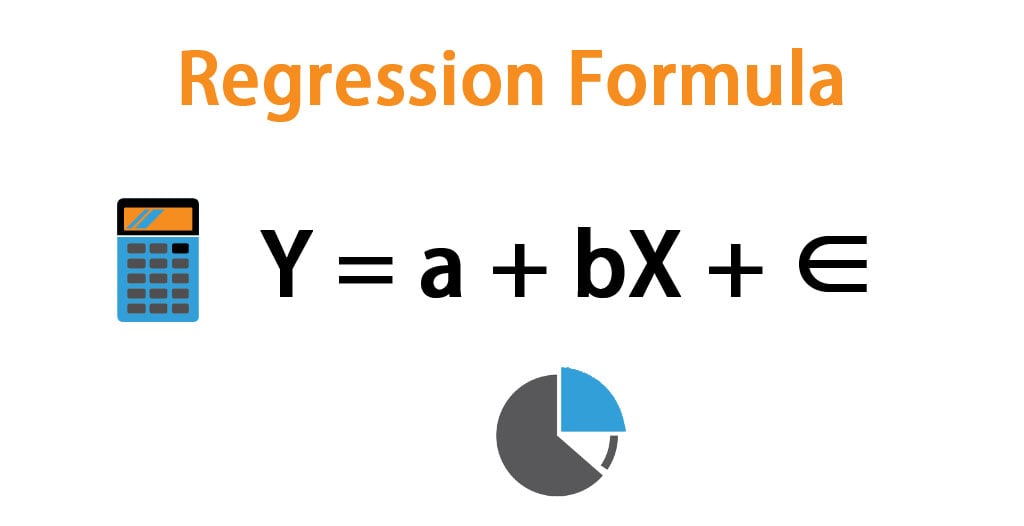Regression analysis is likely the first predictive modeling method you learned as a practitioner during your academic studies or the most common modeling method for your analytics group. Regression concepts were first published in the early 1800s by Adrien‐Marie Legrendre and Carl Gauss. Legrendre was born into a wealthy French family and contributed to a number of advances in the fi elds of mathematics and statistics. Gauss, in contrast, was born to a poor family in Germany. Gauss was a child math prodigy but throughout his life he was reluctant to publish any work that he felt was not above criticism. After his death, many of his personal journals were discovered that detailed his ideas and thoughts. Those ideas were significant advances in the fi eld of mathematics. It is estimated that if Gauss had been more aggressive in publishing his work, he could have advanced the fi eld of mathematics more than 50 years. Those two brilliant men along with Sir R.A. Fischer in the early twentieth century describe the method of regression. The term “regression” was coined by Francis Galton (who was a cousin of Charles Darwin) to describe the biologic process of extreme values moving toward a population mean. A common example of this is children of tall (above‐average height) parents “regressing” toward the mean of the population and being shorter than their parents; conversely children of short (below‐average height) parents being taller than their parents. Prior to Galton, the technique was referred to as “least squares.” From my experience, regression is the most dominant force in driving business decisions today. Regression analysis has many useful characteristics; one is the easy interpretation of results. Regression concepts are widely understood, and the methodology is well developed such that a well‐tuned regression model by a skilled practitioner can outperform many algorithms that are gaining popularity from the machine learning discipline.